Показник F1 у машинному навчанні

Що таке показник F1?

Показник F1 названий на честь свого математичного формулювання, яке включає в себе середнє гармонійне значення достовірністі та пригадування. Середнє гармонійне — це тип середнього, який підкреслює важливість відхилень і часто використовується, коли йдеться про співвідношення або пропорції. У випадку з показником F1, середнє гармонійне значення гарантує, що точність і пригадування враховуються однаково, що призводить до збалансованої оцінки продуктивності моделі.

Показник F1 відіграє ключову роль у сфері машинного навчання, слугуючи ключовою оціночною метрикою для вимірювання точності моделі. На відміну від показника точності, показник F1 поєднує в собі показники достовірністі та здатності до відтворення, пропонуючи більш цілісну оцінку продуктивності моделі.

Оцінка достовірністі, хоч і здається простою, може бути оманливою, особливо коли маєш справу з незбалансованими наборами даних. Розглянемо набір даних бінарної класифікації, де 90% зразків належать до класу 1, а решта 10% — до класу 2. Модель, яка послідовно прогнозує “клас-1”, досягне точності 90%, але вона буде поганим передбачувачем, оскільки не зможе ідентифікувати жодного зразка класу-2.

Щоб вирішити цю проблему, показник F1 встановлює баланс між достовірністю і пригадуванням, забезпечуючи більш справедливу оцінку ефективності моделі. Достовірність вимірює частку позитивних прогнозів, які є точними, в той час як показник пригадування оцінює частку фактично позитивних зразків, які були правильно ідентифіковані.

Хоча в певних ситуаціях між точністю і пригадуванням можуть існувати компроміси, показник F1 має на меті оптимізувати обидва показники одночасно. Високий показник F1 означає, що модель є одночасно точною і вправною у визначенні позитивних зразків.

Як підрахувати результат F1?

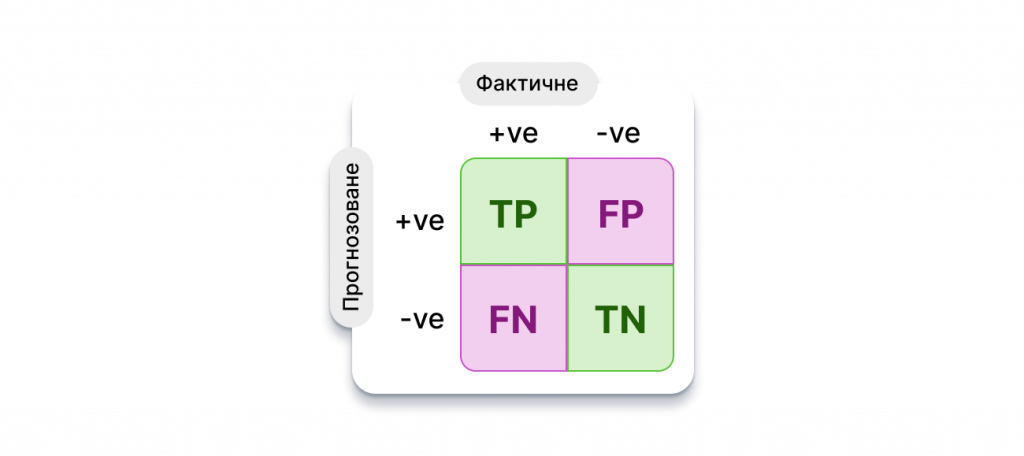
Щоб зрозуміти, як обчислюється показник F1, спочатку потрібно подивитися на матрицю невідповідностей.

Матриця невідповідностей представляє прогнозування продуктивності моделі на наборі даних. Для набору даних бінарних класів (який складається, припустимо, з “позитивних” і “негативних” класів) матриця невідповідностей має чотири основні компоненти:

Істинні позитиви (True Positives, TP): Кількість зразків, які були правильно визначені як “позитивні”.
Хибнопозитивні (False Positives, FP): кількість зразків, які були помилково визначені як “позитивні”.
Істинно негативні (True Negatives, TN): Кількість зразків, правильно визначених як “негативні”.
Хибнонегативні (False Negatives, FN): Кількість зразків, помилково визначених як “негативні”.

Використовуючи компоненти матриці невідповідностей, ми можемо визначити різні метрики, що використовуються для оцінки класифікаторів — точність, достовірність, пригадування та показник F1.

Показник F1 визначається на основі оцінок достовірності та пригадування, які математично визначаються наступним чином:

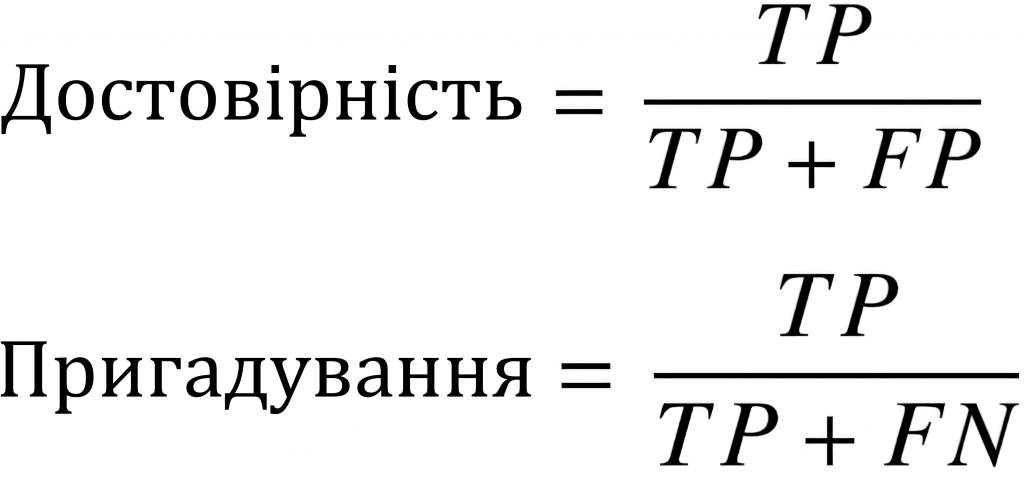
Показник F1 розраховується як середнє гармонійне значення оцінок достовірністі та пригадування, як показано нижче. Він коливається в межах 0-100%, а вищий показник F1 означає кращу якість класифікатора.

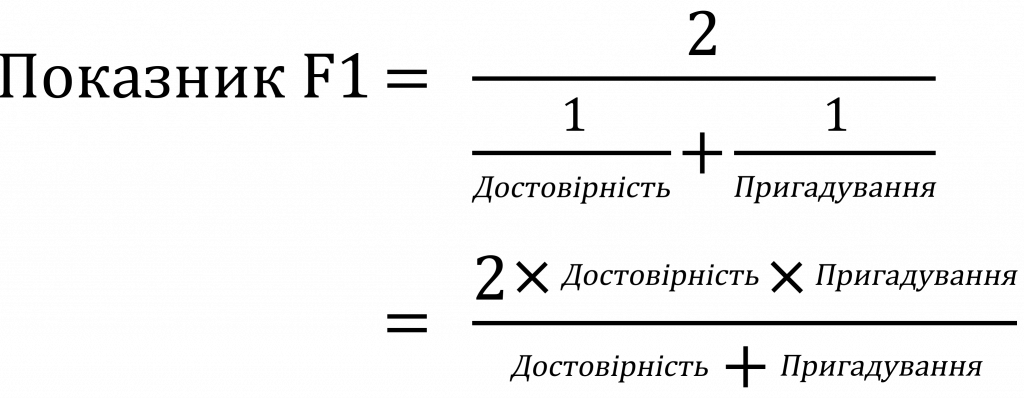
Чому показник F1 обчислюється за допомогою середнього гармонійного значення, а не простого арифметичного або геометричного? Спрощено кажучи, середнє гармонійне заохочує подібні значення для точності та пригадування. Тобто, чим більше показники точності та пригадування відхиляються один від одного, тим гірше середнє гармонійне значення.

З точки зору основних чотирьох елементів матриці невідповідностей, замінивши у наведеному вище рівнянні вирази для оцінок достовірності та пригадування, показник F1 також можна записати таким чином:

Для обчислення показника F1 для багатокласового набору даних використовується метод “один проти всіх” який дозволяє обчислити індивідуальні показники для кожного класу в наборі даних. Береться середнє гармонійне значення для значень точності та пригадування для кожного класу. Потім обчислюється чистий показник F1 за допомогою різних методів усереднення, які ми розглянемо далі.

Макроусереднений показник F1

Макроусереднений показник F1 моделі — це середнє арифметичне отриманих оцінок F1 по класах. Математично це виражається наступним чином (для набору даних з “n” класів):

Макроусереднений показник F1 корисний лише тоді, коли набір даних, що використовується, має однакову кількість точок даних у кожному з класів. Однак більшість реальних наборів даних є незбалансованими за класами — різні категорії мають різну кількість даних. У таких випадках просте середнє може бути оманливою метрикою ефективності.

Мікроусереднений показник F1

Мікроусереднений показник F1 — це метрика, яка підходить за умови багатокласового розподілу даних. Для обчислення метрики використовуються “чисті” (Net) значення TP, FP і FN.

Чистий (Net) TP — це сума оцінок TP набору даних за класами, які обчислюються шляхом розкладання матриці невідповідностей на матриці “один проти всіх”, що відповідають кожному класу.

Якщо ми маємо матрицю невідповідностей, скажімо, “M”, де “M_ij” вказує на елемент для “i” рядка і “j” стовпця, то оцінка мікро F1 може бути математично виражена наступним чином:

Для набору даних бінарних класів оцінка мікроусередненого F1 — це оцінка точності. Давайте розберемося, чому це так. Розглянемо типову матрицю плутанини, як показано нижче.

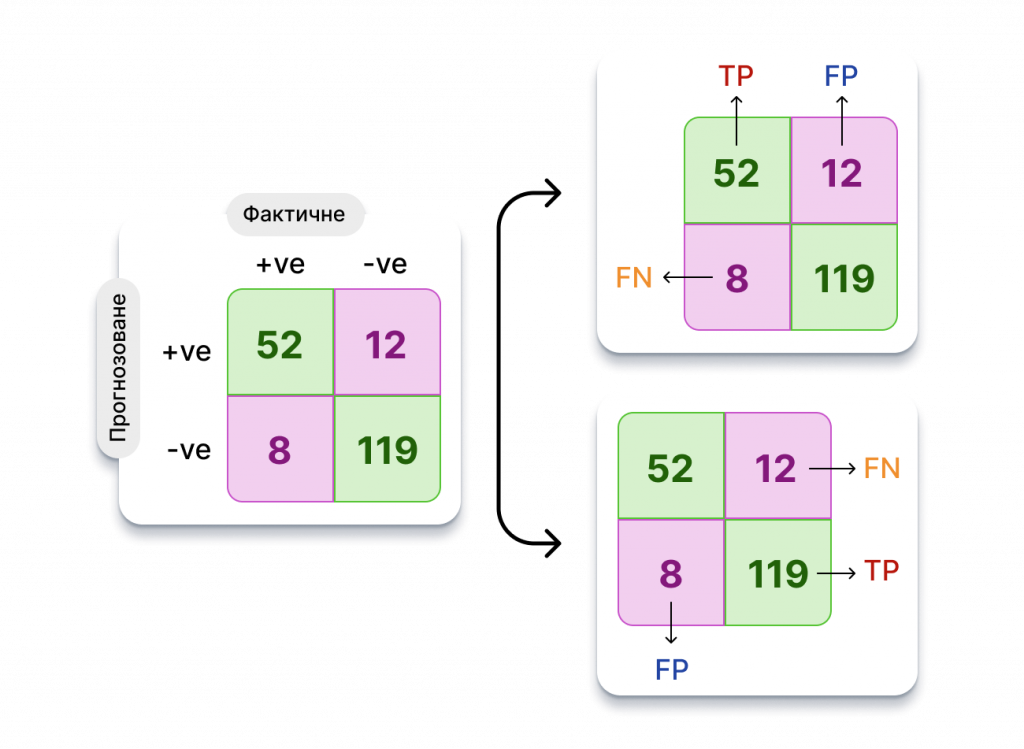
Коли йдеться про позитивний клас, FP дорівнює 12, а FN — 8. Однак для негативного класу початкові FP і FN міняються місцями. Тепер FP дорівнює 8, а FN — 12. Таким чином, математично оцінка мікро F1 стає:

На останньому кроці TP, TN, FP і FN представляють собою початкові визначення компонентів матриці невідповідностей, про які ми говорили на початку цього розділу.

Показник Fβ

Показник Fβ є узагальненою версією показника F1. Він обчислює середнє гармонійне значення, як і оцінка F1, але з пріоритетом, який надається або достовірності, або пригадуванню. “β” — це ваговий коефіцієнт (гіперпараметр, який встановлюється користувачем і завжди більший за 0). Математично це виглядає наступним чином:

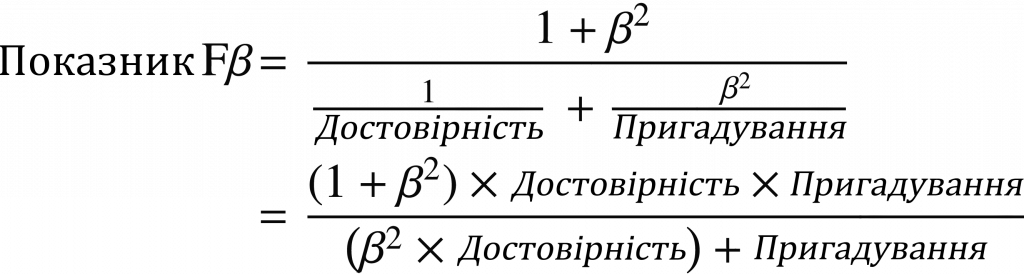
Ми використовуємо показник F1 у випадках, коли β дорівнює 1. Значення β більше 1 сприяє метриці пригадування, тоді як значення менше 1 сприяє метриці достовірності. F0.5 і F2 — це найбільш часто використовувані показники, крім оцінки F1.

Оцінка Fβ корисна, коли ми хочемо надати пріоритет одному показнику, зберігаючи результати іншого показника.

Наприклад, у випадку виявлення COVID-19 хибнонегативні результати є шкідливими, оскільки COVID-позитивному пацієнту ставлять діагноз COVID-негативний, що призводить до поширення хвороби. У цьому випадку показник F2 є більш корисним для мінімізації хибнонегативних результатів, одночасно намагаючись зберегти якомога вищий показник точності. В інших випадках може знадобитися зменшити кількість хибнопозитивних результатів, якщо бажано отримати нижче значення β (наприклад, F0,5).

Як обчислити F-міру у Python?

Результат F1 можна легко обчислити мовою Python за допомогою функції “f1_score” з пакета scikit-learn. Функція приймає на вхід три аргументи (і кілька інших, які ми поки що можемо ігнорувати): істинні підписи, передбачені підписи та “середній” параметр, який може бути бінарним/мікро/макро/зваженим/без параметра.

“Бінарний” режим середнього параметра використовується для отримання специфічної для класу оцінки F1 для набору даних бінарного класу. Як випливає з назви, мікро-, макро- та зважене середнє — це відповідні схеми усереднення для обчислення оцінок для наборів даних з будь-якою кількістю класів. Використання значення “None” повертає всі індивідуальні оцінки F1 для кожного класу. Приклад використання функції наведено нижче.

>>> f1_score (true_labels, predicted_labels, average=None) 
array([0.83870968, 0.84848485, 0.57471264, 0.76190476])

>>> f1_score (true_labels, predicted_labels, average='macro') 
0.7559529828717815

>>> fl_score (true_labels, predicted_labels, average='micro') 
0.7591623036649215

>>> f1_score (true_labels, predicted_labels, average='weighted')
0.7593013943176136

Приклад використання f1_score у Python

Щоб отримати більш повний список метрик одразу, можна скористатися функцією “classification_report” у scikit-learn. Вона приймає істинні та передбачені позначки як вхідні дані і виводить метрики для кожного класу, а також різні середні метрики.

>>> print(classification_report (true_labels, predicted_labels, digits=4)) 
			precision	recall		fl-score	support
1			0.8125		0.8667		0.8387		60
2			0.8750		0.8235		0.8485		34
3			0.5682		0.5814		0.5747		43
4			0.7843		0.7407		0.7619		54

accuracy						0.7592		191
macro avg		0.7600		0.7531		0.7560		191
weighted avg		0.7607		0.7592		0.7593		191

Приклад використання функції classification_report мови Python

Оцінка Fβ може бути обчислена в Python за допомогою функції “fbeta_score“, подібно до функції f1_score, яку ми розглядали вище, з додатковим вхідним аргументом “beta”. Приклад з різними значеннями β наведено нижче:

>>> fbeta_score (true_labels, predicted_labels, average='macro', beta=0.1)
0.7599072173448518

>>> fbeta_score (true_labels, predicted_labels, average='macro', beta=1)
0.7559529828717815

>>> fbeta_score (true_labels, predicted_labels, average='macro', beta=3)
0.7535637200158858

Приклад використання fbeta_score з різними значеннями в Python

Основні висновки

Протягом тривалого часу точність була основним критерієм оцінки моделей машинного навчання.

Однак вона дає дуже мало розуміння тонкощів функціонування моделі, особливо в реальних наборах даних, де ми не маємо достатнього контролю над вибіркою даних. Справедлива оцінка продуктивності моделі так само важлива, як і розробка архітектури моделі для конкретної проблеми.

Оцінка F1 є набагато більш комплексною вимірювальною системою, оскільки вона максимізує дві конкуруючі цілі — точність і швидкість відтворення — одночасно. Показник F1 можна використовувати як для оцінки класу, так і для загальної оцінки. Крім того, інші варіації показника F1, зокрема показник Fβ, дають змогу керувати показником F залежно від поставленої задачі, надаючи пріоритет мінімізації хибнопозитивних або хибнонегативних втрат.

Для обчислення загальної величини F1 для наборів даних використовуються різні методи усереднення, наприклад, мікро-, макро- та вибіркові усереднені величини F. Метрики класу та глобального показника F1 можна легко обчислити за допомогою Python, найпопулярнішої мови для машинного навчання, що робить його однією з найпоширеніших метрик в оцінці ефективності класифікації.